Video: Hoe bewijs je dat de diagonalen van een ruit elkaar halveren?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
In een ruit alle zijden zijn gelijk en overstaande zijden zijn evenwijdig. verder een ruit is ook een parallelgram en vertoont daarom eigenschappen van a parallellogram en dat diagonalen van een parallellogram halveren elkaar.
Dienovereenkomstig, halveren de diagonalen van een ruit elkaar?
In elke ruit , de diagonalen (lijnen die tegenoverliggende hoeken met elkaar verbinden) elkaar halveren haaks (90°). Dat is, elke diagonaal snijdt de ander in twee gelijke delen, en de hoek waar ze elkaar kruisen is altijd 90 graden. Sleep in de bovenstaande afbeelding een willekeurig hoekpunt om de opnieuw vorm te geven ruit en overtuig jezelf ervan dat dit zo is.
Ten tweede, staan ruitdiagonalen loodrecht op elkaar? Eigenschappen van a Ruit De diagonalen zijn loodrecht elkaar in tweeën delen. Aangrenzende hoeken zijn aanvullend (voor bijv. ∠A + ∠B = 180°). EEN ruit is een parallellogram van wie diagonalen zijn loodrecht naar elkaar.
Als je dit in overweging neemt, hoe bewijs je dan dat de diagonalen van een ruit middelloodlijnen zijn?
Een bewijs dat de diagonalen van een ruit staan loodrecht Voortzetting van bovenstaande een bewijs : Overeenkomstige delen van congruente driehoeken zijn congruent, dus alle 4 de hoeken (die in het midden) zijn congruent. Dit leidt ertoe dat ze allemaal gelijk zijn aan 90 graden, en de diagonalen zijn loodrecht naar elkaar.
Is ruit een parallellogram?
DEFINITIE: A ruit is een parallellogram met vier congruente zijden. THEOREM: Als een parallellogram is een ruit , elke diagonaal halveert een paar tegenovergestelde hoeken. THEOREM Converse: Als a parallellogram heeft diagonalen die een paar tegenovergestelde hoeken halveren, het is a ruit.
Aanbevolen:
Wat is een diagonaal in een ruit?
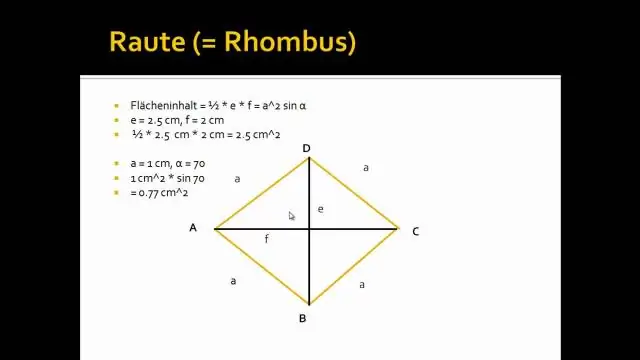
Diagonalen van een ruit In elke ruit snijden de diagonalen (lijnen die tegenover elkaar liggende hoeken met elkaar verbinden) elkaar in een rechte hoek (90°). Dat wil zeggen, elke diagonaal snijdt de andere in twee gelijke delen, en de hoek waar ze elkaar kruisen is altijd 90 graden
Welke van de volgende verwijst naar een reeks op zichzelf staande services die met elkaar communiceren om een werkende softwaretoepassing te maken?
Een servicegeoriënteerde architectuur is een verzameling op zichzelf staande services die met elkaar communiceren om een werkende softwaretoepassing te creëren. In een netwerk met meerdere lagen: het werk van het hele netwerk is verdeeld over verschillende serverniveaus
Snijden diagonalen elkaar altijd in tweeën in een parallellogram?
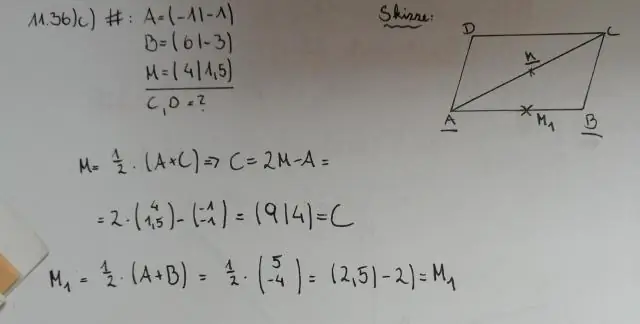
In elk parallellogram snijden de diagonalen (lijnen die tegenovergestelde hoeken met elkaar verbinden) elkaar in tweeën. Dat wil zeggen, elke diagonaal snijdt de andere in twee gelijke delen. Sleep in de bovenstaande afbeelding een willekeurig hoekpunt om het parallellogram opnieuw vorm te geven en overtuig uzelf ervan dat dit zo is
Halveren diagonalen van parallellogram elkaar op 90?
In elke ruit snijden de diagonalen (lijnen die tegenoverliggende hoeken met elkaar verbinden) elkaar in een rechte hoek (90°). Dat wil zeggen, elke diagonaal snijdt de andere in twee gelijke delen, en de hoek waar ze elkaar kruisen is altijd 90 graden
Welke parallellogrammen hebben diagonalen die elkaar halveren?
Als twee aangrenzende zijden van een parallellogram gelijk zijn, dan is het een ruit. Deze test wordt vaak gezien als de definitie van een ruit. Een vierhoek waarvan de diagonalen elkaar loodrecht in tweeën delen, is een ruit