
- Auteur Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:51.
- Laatst gewijzigd 2025-01-22 17:35.
Heap sort is een in-place algoritme. TijdComplexiteit : Tijd complexiteit van heapify is O(Logn). Tijd complexiteit van createAndBuildHeap() is O(n) en algemeen tijd complexiteit van Heap Sort is O(nLogn).
Wat is in dit verband het algoritme van heap sort?
Heap sort algoritme is opgedeeld in twee basisdelen: Het maken van een Hoop van de ongesorteerde lijst/array. Dan een gesorteerd array wordt gemaakt door herhaaldelijk het grootste/kleinste element uit de hoop , en invoegen in de array. De hoop wordt na elke verwijdering gereconstrueerd.
Evenzo, wat is de typische looptijd van een heapsort-algoritme? Quicksort heeft echter een worst-case lopende tijd van O (n 2) O(n^2) O(n2) en een worst-case ruimtecomplexiteit van O (log ? n O(log n O(logn), dus als het erg belangrijk is om een fastworst-case lopende tijd en efficiënt ruimtegebruik, hoopje is de beste optie.
Evenzo wordt gevraagd, wat is de complexiteit van de Heapify-functie?
Het belangrijkste idee is dat in de build_heap algoritme de daadwerkelijke ophopen kosten zijn niet O(log n) voor alle elementen. Wanneer ophopen wordt genoemd, hangt de looptijd af van hoe ver een element in de boom omlaag kan bewegen voordat het proces eindigt. Met andere woorden, het hangt af van de hoogte van het element in de hoop.
Welk sorteeralgoritme heeft de beste asymptotische complexiteit?
Voor Het beste geval inbrengen: Soort en hoop Sorteren is het beste een als hun het beste case runtime complexiteit staat aan). Voor gemiddeld geval: beste asymptotisch looptijd complexiteit is O(nlogn) die wordt gegeven door Samenvoegen Soort , Hoop Soort , Snel Soort . In het ergste geval: het beste looptijd complexiteit is O(nlogn) die wordt gegeven door Merge Soort , Hoop Soort.
Aanbevolen:
Hoe wordt de complexiteit van de samenvoegsortering berekend?
2 antwoorden. Het splitsen van een knoop A[L,R] in twee knopen kost R−L+1 tijd en het vervolgens samenvoegen van de twee onderliggende knopen A[L,M] en A[M+1,R] kost weer A[R&min;L +1] tijd. Dus voor elk knooppunt is het aantal bewerkingen dat het algoritme uitvoert gelijk aan tweemaal de grootte van de array die overeenkomt met dat knooppunt
Wat is het grootste nadeel van het gebruik van het RAD-model?

Wat is het grootste nadeel van het gebruik van het RAD-model? Toelichting: De klant kan een onrealistische productvisie creëren waardoor een team functionaliteit over- of onderontwikkeld. Ook zijn de gespecialiseerde en bekwame ontwikkelaars niet gemakkelijk beschikbaar
Wat zijn de worst case en de gemiddelde complexiteit van de binaire zoekboom?

Binaire zoekboom Algoritme Gemiddelde Slechtste geval Spatie O(n) O(n) Zoeken O(log n) O(n) Voeg O(log n) O(n) Verwijder O(log n) O(n)
Hoe bereken je de complexiteit van de ruimte?
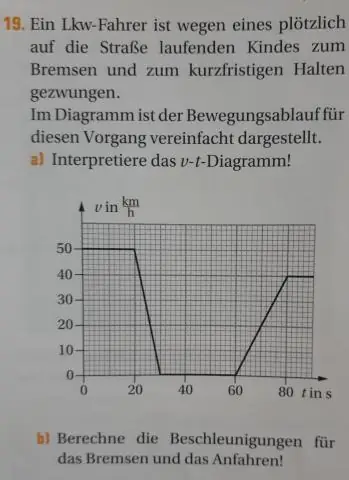
Hulpruimte: is de tijdelijke ruimte (exclusief de invoergrootte) die door uw algoritme is toegewezen om het probleem op te lossen, met betrekking tot invoergrootte. Ruimtecomplexiteit omvat zowel hulpruimte als ruimte die wordt gebruikt door invoer. Ruimtecomplexiteit = invoergrootte + hulpruimte
Wat is de straf in India voor het stelen van activa van computerdocumenten of de broncode van software van een organisatie-individu of van enig ander middel?

Uitleg: De straf in India voor het stelen van computerdocumenten, activa of de broncode van software van een organisatie, persoon of op enige andere manier is 3 jaar gevangenisstraf en een boete van Rs. 500.000
