
- Auteur Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:51.
- Laatst gewijzigd 2025-01-22 17:35.
De vierkant heeft de volgende eigenschappen:
Alle eigenschappen van een ruit zijn van toepassing (degene die hier van belang zijn, zijn parallelle zijden, diagonalen zijn middelloodlijnen van elkaar, en diagonalen halveren de hoeken ). Alle eigenschappen van een rechthoek zijn van toepassing (de enige die hier telt is diagonalen zijn congruent).
Hiervan, zijn diagonalen van een rechthoek bissectrices?
De diagonalen van een rechthoek zal alleen de doorsnijden hoeken als de partijen die elkaar ontmoeten bij de hoek gelijk zijn: met andere woorden, alleen als de rechthoek is een vierkant. Een andere manier om erover na te denken: de hoek is een recht- hoek , en de bissectrice moet half naar rechts komen- hoek naar de zijkanten. vandaar de rechthoek moet vierkant zijn.
Men kan zich ook afvragen of diagonaal of vierkant elkaar halveren? EEN vierkant is een speciaal geval van een gelijkbenig trapezium, vlieger, parallellogram, vierhoek, rechthoek, ruit en trapezium. De diagonalen van een vierkante bissectrice een een ander en staan loodrecht op elkaar (in de afbeelding hierboven in rood weergegeven). Bovendien hebben ze halveren elk paar tegenovergestelde hoeken (geïllustreerd in blauw).
Als je dit in overweging neemt, in welke vierhoeken halveren de diagonalen de hoeken?
EEN vierhoek is een ruit als: het een parallellogram is, en een paar aangrenzende zijden zijn gelijk, het is diagonalen halveren elkaar rechts hoeken , zijn diagonalen halveren elk hoekpunt hoek.
Wat is de diagonaal van vierkant?
diagonalen van een vierkant . EEN vierkant heeft twee diagonalen , dit zijn lijnsegmenten die tegenoverliggende hoekpunten (hoeken) van de met elkaar verbinden vierkant . Met andere woorden, het punt waar de diagonalen snijden (kruis), verdeelt elk diagonaal in twee gelijke delen. Elk diagonaal verdeelt de vierkant in twee congruente gelijkbenige rechthoekige driehoeken.
Aanbevolen:
Zijn diagonalen van vierkant gelijk?
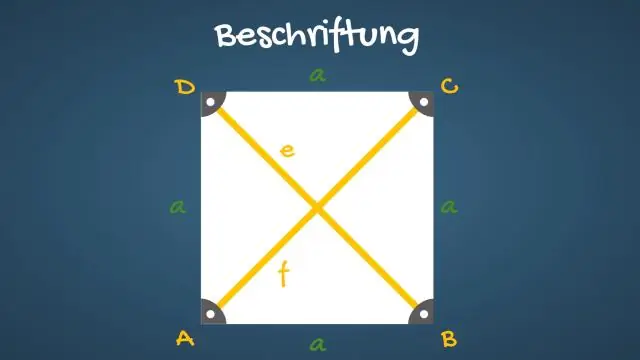
De diagonalen van een vierkant halveren de hoeken. Overstaande zijden van een vierkant zijn evenwijdig en even lang. Alle vier zijden van een vierkant zijn gelijk. De diagonalen van een vierkant zijn gelijk
Zijn de twee diagonalen van een parallellogram gelijk?

Wanneer een parallellogram in twee driehoeken wordt verdeeld, krijgen we te zien dat de hoeken over de gemeenschappelijke zijde (hier de diagonaal) gelijk zijn. Dit bewijst dat de overstaande hoeken in een parallellogram ook gelijk zijn. De diagonalen van een parallellogram zijn niet even lang
Hoeveel kost het om een huis van 2000 vierkante meter te bedraden?
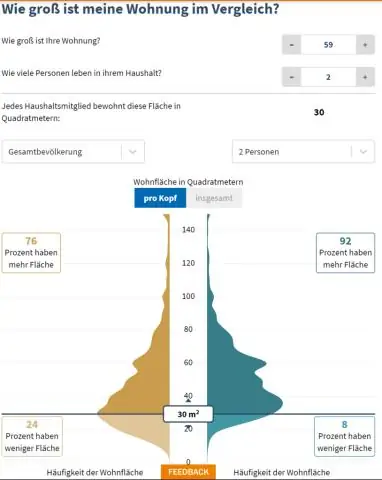
De kosten voor het opnieuw bedraden van een huis van 1.000 m² bedragen $ 2.000 tot $ 6.000, of ongeveer $ 2 tot $ 4 per vierkante voet. Een huis van meer dan 2500 vierkante meter opnieuw bedraden. Kosten om een huis opnieuw te bedraden per vierkante voet. Vierkante voet gemiddelde kosten 1.500 $ 2.300 - $ 5.600 2.000 $ 3.200 - $ 7.600 2.500 $ 3.900 - $ 9.400 3.000 $ 4.800 - $ 11.400
Hoe verwijder je een vierkante buisplug?

Als een plug met vierkante kop moet worden verwijderd, sla dan op de kop van de plug met een hamer van één pond. Ritmische slagen, niet te hard, moeten een minuut of langer worden gebruikt. Een spray-penetrant, zoals WD-40, helpt altijd. Gebruik een grote sleutel, zoals een 12' halve maan om de plug te verwijderen
Waarom heeft een vierkante mozaïek?

Slechts drie regelmatige veelhoeken mozaïek: gelijkzijdige driehoeken, vierkanten en regelmatige zeshoeken. Geen enkele andere regelmatige veelhoek kan mozaïeken vanwege de hoeken van de hoeken van de veelhoeken. Voor regelmatige veelhoeken betekent dit dat de hoek van de hoeken van de veelhoek 360 graden moet delen
