Video: Zijn de twee diagonalen van een parallellogram gelijk?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
Wanneer een parallellogram is verdeeld in twee driehoeken krijgen we te zien dat de hoeken over de gemeenschappelijke zijde (hier de diagonaal ) zijn Gelijk . Dit bewijst dat de overstaande hoeken in a parallellogram zijn ook Gelijk . De diagonalen van een parallellogram zijn niet van Gelijk lengte.
Net zo, zijn diagonalen van een parallellogram congruent?
Alle eigenschappen van a parallellogram toepassen (degenen die hier van belang zijn, zijn parallelle zijden, tegenovergestelde zijden zijn congruent , en diagonalen elkaar doormidden snijden). Alle hoeken zijn per definitie rechte hoeken. De diagonalen zijn congruent.
Men kan zich ook afvragen, waarom zijn de diagonalen van een parallellogram niet congruent? De diagonalen van een parallellogram zijn niet Gelijk. Omdat de parallellogram heeft aangrenzende hoeken als scherp en stomp, de diagonalen splits de figuur in 2 paren van congruent driehoeken. Omdat de hoeken scherp of stomp zijn, zijn twee van de kortere zijden van de driehoeken, zowel scherp als stomp, congruent.
Evenzo, wat is de diagonaal van een parallellogram?
Diagonaal van Parallellogram Formule A parallellogram is een vierhoek waarvan de overstaande zijden evenwijdig en gelijk zijn. De overstaande zijden zijn evenwijdig en gelijk en vormen gelijke hoeken aan de overstaande zijden. diagonalen van a parallellogram zijn de segmenten die de tegenoverliggende hoeken van de figuur verbinden.
Zijn de twee diagonalen van een rechthoek gelijk Waarom?
De twee diagonalen congruent zijn (dezelfde lengte). Elk diagonaal snijdt de andere doormidden. Met andere woorden, het punt waar de diagonalen snijden (kruis), verdeelt elk diagonaal naar binnen twee gelijk onderdelen. Elk diagonaal verdeelt de rechthoek naar binnen twee congruente rechthoekige driehoeken.
Aanbevolen:
Zijn diagonalen van vierkant gelijk?
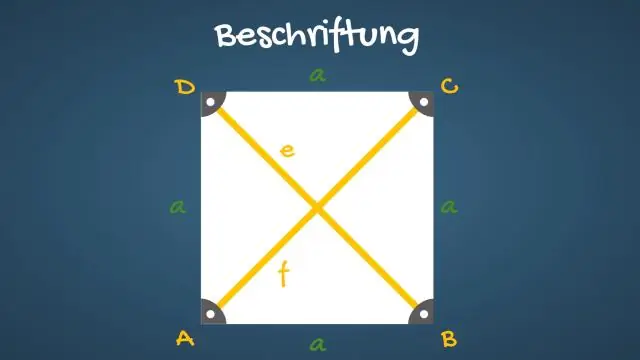
De diagonalen van een vierkant halveren de hoeken. Overstaande zijden van een vierkant zijn evenwijdig en even lang. Alle vier zijden van een vierkant zijn gelijk. De diagonalen van een vierkant zijn gelijk
Zijn twee arrays gelijk aan JavaScript?
Om in Javascript twee arrays te vergelijken, moeten we controleren of de lengte van beide arrays hetzelfde moet zijn, dat de objecten die erin aanwezig zijn van hetzelfde type zijn en dat elk item in de ene array gelijk is aan de tegenhanger in een andere array. Door dit te doen, kunnen we concluderen dat beide arrays hetzelfde zijn of niet. JavaScript biedt een functie JSON
Snijden diagonalen elkaar altijd in tweeën in een parallellogram?
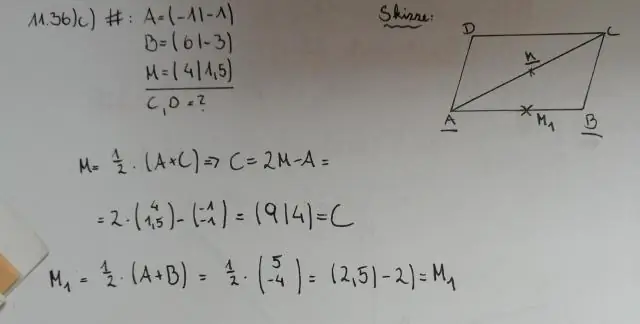
In elk parallellogram snijden de diagonalen (lijnen die tegenovergestelde hoeken met elkaar verbinden) elkaar in tweeën. Dat wil zeggen, elke diagonaal snijdt de andere in twee gelijke delen. Sleep in de bovenstaande afbeelding een willekeurig hoekpunt om het parallellogram opnieuw vorm te geven en overtuig uzelf ervan dat dit zo is
Halveren diagonalen van parallellogram elkaar op 90?
In elke ruit snijden de diagonalen (lijnen die tegenoverliggende hoeken met elkaar verbinden) elkaar in een rechte hoek (90°). Dat wil zeggen, elke diagonaal snijdt de andere in twee gelijke delen, en de hoek waar ze elkaar kruisen is altijd 90 graden
Zijn twee objecten altijd gelijk wanneer hun methode CompareTo () nul retourneert?
Het wordt aanbevolen dat CompareTo alleen 0 retourneert, als een aanroep naar is gelijk aan op dezelfde objecten true zou retourneren: CompareTo(e2) == 0 heeft dezelfde Booleaanse waarde als e1. is gelijk aan (e2) voor elke e1 en e2 van klasse C. Merk op dat null geen instantie is van een klasse, en e