
Inhoudsopgave:
- Auteur Lynn Donovan donovan@answers-technology.com.
- Public 2024-01-18 08:27.
- Laatst gewijzigd 2025-01-22 17:35.
- Verdeling de eerste term van de teller door de eerste term van de noemer, en zet die in het antwoord.
- Vermenigvuldig de noemer met dat antwoord, zet dat onder de teller.
- Aftrekken om een nieuwe te maken polynoom .
Hoe deel je op deze manier een polynoom door een binomiaal?
Lange deling van een veelterm door een binomiaal
- Deel de hoogste graadterm van de veelterm door de hoogste graadterm van de binomiaal.
- Vermenigvuldig dit resultaat met de deler en trek de resulterende binomiaal af van de veelterm.
- Deel de hoogste graadterm van de resterende polynoom door de hoogste graadterm van de binomiaal.
Weet ook, werkt synthetische deling altijd? Synthetische Divisie . synthetische divisie is een steno, of snelkoppeling, methode van polynomiale deling in het speciale geval van delen door een lineaire factor -- en het is alleen werken in dit geval. synthetische divisie wordt echter over het algemeen niet gebruikt om factoren uit te splitsen, maar om nullen (of wortels) van veeltermen te vinden.
Evenzo, hoe deel je veeltermen door veeltermen?
Stap 2: Verdeling de term met de hoogste macht binnen de afdeling symbool door de term met de hoogste macht buiten de afdeling symbool. In dit geval hebben we x3 gedeeld door x dat is x2. Stap 3: Vermenigvuldig (of verdeel) het antwoord verkregen in de vorige stap met de polynoom voor de afdeling symbool.
Hoe verdeel je Monomials?
Tot verdeling een monomiaal door een monomiaal , verdeling de coëfficiënten (of vereenvoudig ze zoals je een breuk zou doen) en verdeling de variabelen met gelijke basen door hun exponenten af te trekken. Tot verdeling een polynoom door a monomiaal , verdeling elke term van de polynoom door de monomiaal . Let goed op de borden!
Aanbevolen:
Hoe noem je een polynoom met 6 termen?
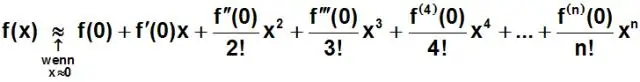
De volgende namen worden toegewezen aan polynomen op basis van hun graad: Graad 4 – quartic (of, als alle termen een even graad hebben, bikwadraat) Graad 5 – quintic. Graad 6 - sextisch (of, minder vaak, hexisch)
Wat is een eerstegraads polynoom?
Eerstegraads veeltermen. Eerstegraads polynomen worden ook wel lineaire polynomen genoemd. In het bijzonder zijn eerstegraads polynomen lijnen die noch horizontaal noch verticaal zijn. Vaker wordt de letter m gebruikt als de coëfficiënt van x in plaats van a, en wordt deze gebruikt om de helling van de lijn weer te geven
Wat is een 3e graads polynoom?

Derdegraads veeltermen zijn ook bekend als kubieke veeltermen. Cubics hebben de volgende kenmerken: Eén tot drie wortels. Twee of nul extrema. Wortels zijn oplosbaar door radicalen
Is Pi een polynoom?

Pi (π) wordt niet als een polynoom beschouwd. Het is een waarde die verwijst naar de omtrek van een cirkel. Aan de andere kant verwijst polynoom naar een vergelijking die vier variabelen of meer bevat
Hoe kun je zien of een uitdrukking een polynoom is?

Om een uitdrukking een polynoomterm te laten zijn, moeten alle variabelen in de uitdrukking gehele getallen hebben (of anders de 'begrepen' macht van 1, zoals in x1, die normaal wordt geschreven als x). Een gewoon getal kan ook een veelterm zijn
