Video: Wat is de waarheidstabel van een Biconditional?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
Om u te helpen herinneren aan de waarheidstabellen voor deze uitspraken kun je het volgende bedenken: De voorwaardelijke, p impliceert q, is alleen onwaar als de voorkant waar is maar de achterkant onwaar. Anders is het waar. De biconditioneel , p iff q, is waar wanneer de twee uitspraken hetzelfde hebben waarheid waarde.
Ook gevraagd, wat is de waarheidswaarde van een Biconditional statement?
Definitie: A bivoorwaardelijke verklaring is gedefinieerd om te zijn waar wanneer beide delen hetzelfde hebben waarheidswaarde . De biconditioneel operator wordt aangegeven met een dubbele pijl. De biconditioneel p q staat voor "p als en slechts als q", waarbij p een hypothese is en q een conclusie.
Bovendien, wat betekent de pijl in waarheidstabellen? Het is een symbool dat twee proposities verbindt in de context van proposities logica (en zijn extensies, eerste orde) logica , enzovoort). De waarheidstabel van → is gedefinieerd als zijnde dat p→q onwaar is als en slechts als p waar is en q onwaar is.
Waarvoor wordt naast bovenstaande een waarheidstabel gebruikt?
EEN waarheidstabel is een wiskundige tafel vroeger bepalen of een samengestelde verklaring waar of onwaar is. In een waarheidstabel , wordt elke instructie meestal weergegeven door een letter of variabele, zoals p, q of r, en elke instructie heeft ook zijn eigen corresponderende kolom in de waarheidstabel dat somt alle mogelijke op waarheid waarden.
Wat is een voorbeeld van een Biconditional statement?
Voorbeelden van bivoorwaardelijke verklaringen De bivoorwaardelijke uitspraken voor deze twee verzamelingen zou zijn: De veelhoek heeft slechts vier zijden dan en slechts dan als de veelhoek een vierhoek is. De veelhoek is een vierhoek dan en slechts dan als de veelhoek maar vier zijden heeft.
Aanbevolen:
Wat is een proces in een besturingssysteem, wat is een thread in een besturingssysteem?
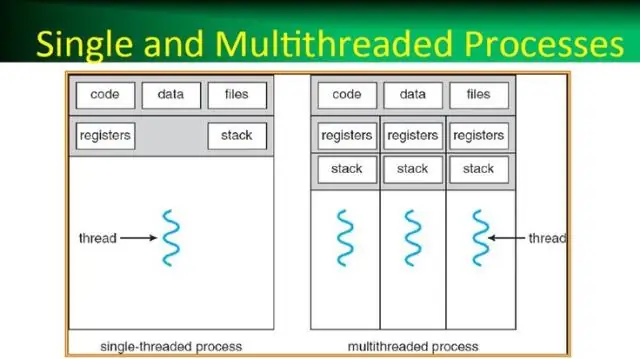
Een proces, in de eenvoudigste bewoordingen, is een uitvoeringsprogramma. Een of meer threads worden uitgevoerd in de context van het proces. Een thread is de basiseenheid waaraan het besturingssysteem processortijd toewijst. De threadpool wordt voornamelijk gebruikt om het aantal applicatiethreads te verminderen en om de workerthreads te beheren
Uit hoeveel rijen bestaat een waarheidstabel?
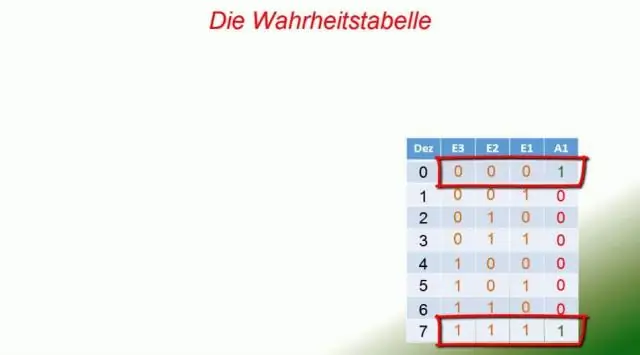
Een waarheidstabel van N inputs bevat 2N rijen, één voor elke mogelijke waarde van de inputs. Elke rij in een waarheidstabel is gekoppeld aan een minterm die WAAR is voor die rij
Worden gedefinieerd als de relatie tussen eigenschappen van een object en de mogelijkheden van een agent die aanwijzingen geven voor het gebruik van een object?
Een aanbod is een relatie tussen de eigenschappen van een object en de mogelijkheden van de agent die bepalen hoe het object mogelijk kan worden gebruikt
Wat is een voordeel van het hebben van een domeinmodelnetwerk in tegenstelling tot een werkgroep?
Werkgroep heeft snellere en betrouwbaardere aanmeldingen, domein heeft langzamere aanmeldingen en als de server uitvalt, zit u vast. Met domeingebaseerde toegang is het eenvoudiger om gebruikers te beheren, updates te implementeren en back-ups te beheren (vooral bij gebruik van mapomleiding)
Wat is de straf in India voor het stelen van activa van computerdocumenten of de broncode van software van een organisatie-individu of van enig ander middel?
Uitleg: De straf in India voor het stelen van computerdocumenten, activa of de broncode van software van een organisatie, persoon of op enige andere manier is 3 jaar gevangenisstraf en een boete van Rs. 500.000