
- Auteur Lynn Donovan donovan@answers-technology.com.
- Public 2023-12-15 23:51.
- Laatst gewijzigd 2025-01-22 17:35.
In de wiskunde, een injectief functie (ook bekend als injectie of één-op-één-functie) is een functie die verschillende elementen van zijn domein toewijst aan verschillende elementen van zijn codomein. Met andere woorden, elk element van het codomein van de functie is het beeld van ten hoogste één element van zijn domein.
Evenzo kunt u zich afvragen, wat is een voorbeeld van een injectiefunctie?
Voorbeeld : De functie f(x) = x2van de verzameling positieve reële getallen naar positieve reële getallen is beide injectief en surjectief. Zo is het ook bijectief . Maar hetzelfde functie uit de verzameling van alle reële getallen is niet bijectief omdat we dat hadden kunnen doen, want voorbeeld , beide.
Bovendien, hoe bewijs je Surjectief en Injectief? omdat f een bijectie is. Tot bewijzen een functie is bijjectief, je moet bewijzen dat is het injectief en ook surjectief . " injectief " betekent dat er geen twee elementen in het domein van de functie worden toegewezen aan dezelfde afbeelding." Surjectief " betekent dat elk element in het bereik van de functie wordt geraakt door de functie.
Dienovereenkomstig, is de lege functie injectief?
Volgens deze definitie is elke lege functie is niet injectief omdat ˘f:S→∅ geen. is functie.
Hoe weet je of een functie grafisch is?
Voor één-één: trek gewoon verticale lijnen (loodrecht op de x-as) en als je een verticale lijn vindt die de kromme van functie dan is het niet één. Wat betreft één-één moet elke verticale lijn de. kruisen grafiek van functie op een bepaald moment!
Aanbevolen:
Wat betekent S op Instax Mini 9?

Aan de achterzijde zie je dat de filmtellerweergave (het aantal resterende opnames) op S staat. Dit komt doordat je het zwarte filmdeksel nog moet uitwerpen. Om dit te doen, zet u gewoon de camera aan door op de grote knop direct naast de lens te drukken en drukt u op de ontspanknop
Wat betekent set in SAS?

SET leest een observatie uit een bestaande SAS-dataset. INPUT leest onbewerkte gegevens uit een extern bestand of in-stream datalijnen om SAS-variabelen en observaties te creëren. Door de KEY=-optie te gebruiken met SET kunt u waarnemingen niet-opeenvolgend in een SAS-gegevensset openen op basis van een waarde
Wat betekent CLS in batchbestand?

Type: Commando
Wat betekent klasseobject in Python?

Een klasse is een codesjabloon voor het maken van objecten. Objecten hebben lidvariabelen en daaraan is gedrag gekoppeld. In python wordt een klasse gemaakt door de trefwoordklasse. Een object wordt gemaakt met behulp van de constructor van de klasse. Dit object wordt dan de instantie van de klasse genoemd
Wat betekent servicestof?
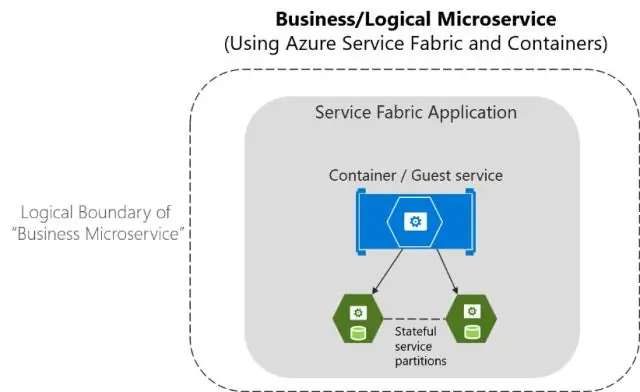
Azure Service Fabric is een gedistribueerd systeemplatform waarmee u eenvoudig schaalbare en betrouwbare microservices en containers kunt verpakken, implementeren en beheren. Service Fabric vertegenwoordigt het platform van de volgende generatie voor het bouwen en beheren van deze enterprise-class, tier-1, cloud-scale applicaties die in containers worden uitgevoerd
