Video: Hoe vind je het kortste pad in een gerichte graaf?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
Gegeven een gewogen geregisseerd acyclisch grafiek en een bronvertex in de grafiek , vind de kortste paden van de gegeven bron naar alle andere hoekpunten.
Kortste pad in gerichte acyclische grafiek
- Initialiseer dist = {INF, INF, ….}
- Maak een toplogische volgorde van alle hoekpunten.
- Doe het volgende voor elk hoekpunt u in topologische volgorde.
Hoe vind je op deze manier het kortste pad in een grafiek?
De algoritmestappen: voor a grafiek met hoekpunten: Initialiseer de kortste paden tussen alle hoekpunten met Infinity. Vind alle paar kortste paden die tussenliggende hoekpunten gebruiken, dan vind de kortste paden die tussenliggende vertex gebruiken enzovoort. totdat alle hoekpunten als tussenliggende knooppunten worden gebruikt.
Hoe vind je naast het bovenstaande het kortste pad in DFS? Nee, u kunt niet gebruiken DFS tot vind de kortste weg in een ongewogen grafiek. Het is niet zo dat, vinden de Kortste weg tussen twee knooppunten wordt exclusief opgelost door BFS.
Evenzo, hoe vind je het kortste pad in een boom?
- Traverse boom (diepte eerst)
- Houd de indexen (knooppunten)
- voeg de waarden toe.
- doe (1) tot het einde van de boom.
- vergelijk de som en print het pad en de som.
Welk algoritme wordt gebruikt om de kortste weg te vinden?
Dijkstra's Shortest Path First-algoritme
Aanbevolen:
Wat is een fysiek pad en een virtueel pad in asp-net?
Laten we eerst het overzicht van beide bekijken. Fysiek pad - Dit is het werkelijke pad waarin het bestand zich bevindt door IIS. Virtueel pad - Dit is het logische pad om toegang te krijgen tot het bestand waarnaar wordt verwezen van buiten de IIS-toepassingsmap
Hoe graaf je een brievenbus uit?
Haal de post van je brievenbus van de grond. Graaf rond je post met je schop. Geef de grond in en rond je gat en brievenbuspost water om de grond los te maken. Wiebel en trek aan je brievenbuspost. Schroef uw houten stuk van 2 inch bij 4 inch in een hoek van 90 graden op de brievenbuspost
Hoe gebruik ik BFS om het kortste pad te vinden?
Om het kortste pad te vinden, hoeft u alleen maar bij de bron te beginnen en eerst een uitgebreide zoekopdracht uit te voeren en te stoppen wanneer u uw bestemmingsknooppunt vindt. Het enige extra dat u hoeft te doen, is een array previous[n] hebben die het vorige knooppunt voor elk bezocht knooppunt opslaat. De vorige van de bron kan nul zijn
Hoe vind ik het MySQL-pad in Windows?
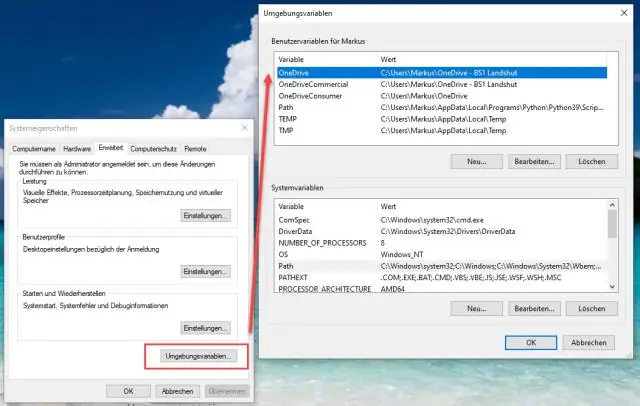
Klik op het Windows-bureaublad met de rechtermuisknop op het pictogram Deze computer en selecteer Eigenschappen. Selecteer vervolgens het tabblad Geavanceerd in het menu Systeemeigenschappen dat verschijnt en klik op de knop Omgevingsvariabelen. Selecteer onder Systeemvariabelen Pad en klik vervolgens op de knop Bewerken. Het dialoogvenster Systeemvariabele bewerken zou moeten verschijnen
Hoe gebruik je Dijkstra's kortste pad-algoritme?
Dijkstra's algoritme om de kortste weg tussen a en b te vinden. Het kiest het niet-bezochte hoekpunt met de laagste afstand, berekent de afstand erdoorheen naar elke niet-bezochte buur en werkt de afstand van de buur bij als deze kleiner is. Markeer bezocht (ingesteld op rood) als je klaar bent met buren