Video: Wat zijn de toepassingen van de driehoek van Pascal?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
De driehoek van Pascal is meer dan alleen een grote driehoek van cijfers. Er zijn twee belangrijke gebieden waar: De driehoek van Pascal is gebruikt , in Algebra en inWaarschijnlijkheid / Combinatoriek. Laten we zeggen dat je de polynoom x+1 hebt, en je wilt het verhogen tot een aantal machten, zoals 1, 2, 3, 4, 5,.
Bovendien, hoe werkt de driehoek van Pascal?
Op het puntje van De driehoek van Pascal is het getal 1, dat de nulde rij vormt. De eerste rij (1 & 1) bevat twee enen, beide gevormd door de twee getallen erboven links en rechts op te tellen, in dit geval 1 en 0 (alle getallen buiten de Driehoek zijn nullen). Op deze manier worden de rijen van de driehoek oneindig doorgaan.
Evenzo, hoe verhoudt de driehoek van Pascal zich tot combinaties? Combinaties kan herhaling of geen herhaling hebben. De inzendingen in De driehoek van Pascal zijn eigenlijk het aantal combinaties van N neem n waarbij N het rijnummer is dat begint met N = 0 voor de bovenste rij en n het nde getal is in de rij die van links naar rechts telt, waarbij het n = 0 getal het eerste getal is.
Evenzo, welke banen gebruiken de driehoek van Pascal?
Vandaag, pascal s driehoek wordt over het algemeen gebruikt door ontwerpers om complexe en nauwkeurige berekeningen te maken in veel aspecten van wiskunde, maar wordt voornamelijk gebruikt in algebra en kansrekening. Banen dat vaak gebruik maken van de driehoek zou architecten, grafisch ontwerpers, financiën, kaarten, enz.
Hoe worden Fibonacci-getallen gebruikt in de driehoek van Pascal?
De nummers op diagonalen van de driehoek toevoegen aan de Fibonacci-reeks , zoals hieronder weergegeven. De driehoek van Pascal heeft veel ongebruikelijke eigenschappen en een verscheidenheid aan toepassingen: de horizontale rijen vertegenwoordigen machten van 11 (1, 11, 121, 1331, 14641) voor de eerste 5 rijen, waarbij de nummers hebben slechts één cijfer.
Aanbevolen:
Wat zijn de drie hoeken van de semantische driehoek?
In zijn drie hoeken beeldt de semantische driehoek drie noodzakelijke elementen uit om de betekenis in taal te identificeren. Het eerste element is het symbool, de connotatieve betekenis van het woord. In de tweede hoek staat de verwijzing, de connotatieve betekenis van het woord
Wat zijn de toepassingen van multiplexer en demultiplexer?
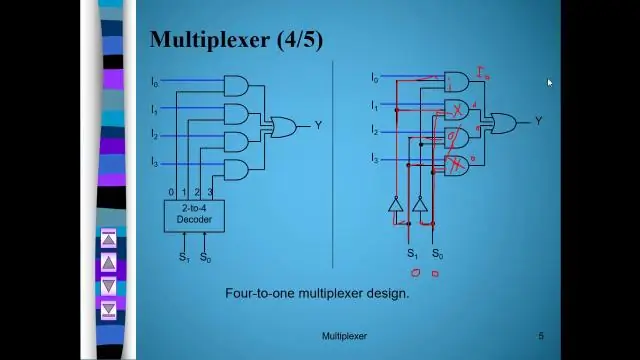
Deze toepassingen omvatten het volgende: Communicatiesysteem - Multiplexer en Demultiplexer worden beide gebruikt in communicatiesystemen om het proces van gegevensoverdracht uit te voeren. Een de-multiplexer ontvangt de uitgangssignalen van de multiplexer; en aan de ontvangerzijde converteert het ze terug naar de oorspronkelijke vorm
Wat zijn de toepassingen van Android Studio?
Android Studio is de officiële IDE van Android. Het is speciaal gebouwd voor Android om uw ontwikkeling te versnellen en u te helpen bij het bouwen van apps van de hoogste kwaliteit voor elk Android-apparaat. Het biedt tools die op maat zijn gemaakt voor Android-ontwikkelaars, waaronder tools voor het bewerken van rich code, debuggen, testen en profileren
Wat zijn de toepassingen van internet in onderzoek?
Veelvoorkomende toepassingen van internetonderzoek zijn persoonlijk onderzoek over een bepaald onderwerp (iets dat in het nieuws wordt genoemd, een gezondheidsprobleem, enz.), studenten die onderzoek doen voor academische projecten en papers, en journalisten en andere schrijvers die onderzoek doen naar verhalen. Onderzoek is een breed begrip
Wat zijn de toepassingen van super-trefwoord in Java?
Gebruik van Java super Trefwoord super kan worden gebruikt om te verwijzen naar een directe instantievariabele van de bovenliggende klasse. super kan worden gebruikt om de directe bovenliggende klassenmethode aan te roepen. super() kan worden gebruikt om de constructor van de onmiddellijke bovenliggende klasse aan te roepen