Video: Hoe berekent Lstm het aantal parameters?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
Dus, volgens uw waarden. Als je het in de formule invoert, krijg je: ->(n=256, m=4096), totaal aantal parameters is 4*((256*256) + (256*4096) + (256)) = 4*(1114368) = 4457472. De nummer van gewichten is 28 = 16 (num_units * num_units) voor de terugkerende verbindingen + 12 (input_dim * num_units) voor invoer.
Ook gevraagd, hoe vind je het aantal parameters?
Tot berekenen het leerbare parameters hier hoeven we alleen maar te vermenigvuldigen met de vorm van breedte m, hoogte n en rekening te houden met al dergelijke filters k. Vergeet de bias-term voor elk van de filters niet. Aantal parameters in een CONV-laag zou zijn: ((m * n)+1)*k), toegevoegd 1 vanwege de bias-term voor elk filter.
Evenzo, hoeveel verborgen eenheden heeft Lstm? Een LSTM netwerk. Het netwerk heeft vijf ingangen: eenheden , een verborgen laag samengesteld uit twee LSTM geheugenblokken en drie output eenheden . Elk geheugenblok heeft vier ingangen, maar slechts één uitgang.
Vervolgens kan men zich ook afvragen, hoe vind je het aantal parameters in RNN?
1 Antwoord. De entiteiten W, U en V worden gedeeld door alle stappen van de RNN en dit zijn de enige parameters in het model beschreven in de figuur. Vandaar aantal parameters te leren tijdens de training = dim(W)+dim(V)+dim(U). Op basis van gegevens in de vraag is dit = n2+kn+nm.
Hoeveel lagen heeft Lstm?
Over het algemeen, 2 lagen hebben aangetoond voldoende te zijn om complexere kenmerken te detecteren. Meer lagen kan beter, maar ook moeilijker te trainen zijn. Als algemene vuistregel - 1 verborgen laag werk met eenvoudige problemen, zoals deze, en twee zijn voldoende om redelijk complexe functies te vinden.
Aanbevolen:
Hoe berekent Eclipse regels code?
Een mogelijke manier om regels code te tellen in Eclipse: gebruik het menu Zoeken / Bestand, selecteer het tabblad Bestand zoeken, specificeer [s]* voor Tekst bevat (dit telt geen lege regels) en vink Reguliere expressie aan. het integreert in eclipse als externe code metrische tool, het is echter niet real-time, het genereert een rapport
Wat is het proces van het definiëren van twee of meer methoden binnen dezelfde klasse met dezelfde naam maar met verschillende parameters?
Overbelasting van de methode De handtekening van een methode bestaat niet uit het retourtype, de zichtbaarheid of de uitzonderingen die het kan veroorzaken. De praktijk van het definiëren van twee of meer methoden binnen dezelfde klasse die dezelfde naam hebben maar verschillende parameters hebben, wordt overbelastingsmethoden genoemd
Hoe berekent Round Robin de gemiddelde wachttijd?
U kunt de wachttijd berekenen door een Gantt-diagram te tekenen, zodat de wachttijd van het proces gelijk is aan de voltooiingstijd - (aankomsttijd + burst-tijd). De laatste starttijd van P1 is 24 (wanneer P1 voor de 3e keer in Gannt-diagram wordt uitgevoerd) P1 is 2 keer in zijn leven vooruitgeschoven Quantum = 4, aankomst = 0
Hoe berekent Linux het CPU-gebruik per proces?
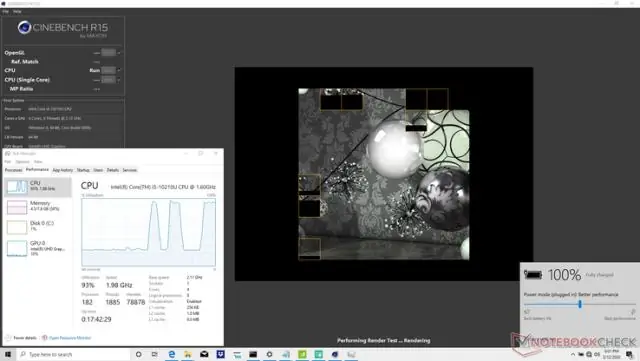
Hoe wordt het totale CPU-gebruik berekend voor een Linux-servermonitor? CPU-gebruik wordt berekend met het 'top'-commando. CPU-gebruik = 100 - inactieve tijd. inactieve waarde = 93,1. CPU-gebruik = (100 - 93,1) = 6,9% Als de server een AWS-instantie is, wordt het CPU-gebruik berekend met de formule:
Hoe berekent SQL Server IOPS?
IOPS is eigenlijk gelijk aan de wachtrijdiepte gedeeld door de latentie, en IOPS op zichzelf houdt geen rekening met de overdrachtsgrootte voor een afzonderlijke schijfoverdracht. U kunt IOPS vertalen naar MB/sec en MB/sec naar latentie zolang u de wachtrijdiepte en overdrachtsgrootte kent