Video: Waar wordt het Prims-algoritme voor gebruikt?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
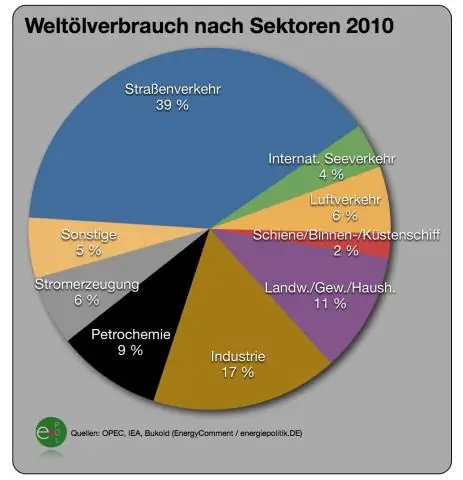
In de informatica, Prim's (ook bekend als Jarník's) algoritme is een hebzuchtig algoritme die een minimale opspannende boom vindt voor een gewogen ongerichte graaf. Dit betekent dat het een subset van de randen vindt die een boom vormt die elk hoekpunt omvat, waarbij het totale gewicht van alle randen in de boom wordt geminimaliseerd.
Trouwens, waar wordt het algoritme van Kruskal voor gebruikt?
Kruskal's algoritme gebruikt de hebzuchtige benadering om een minimaal opspannende boom te vinden. Kruskal's algoritme behandel elke knoop als een onafhankelijke boom en verbindt de ene met de andere alleen als dit de laagste kosten heeft in vergelijking met alle andere beschikbare opties.
Ten tweede, wat doet Dijkstra's algoritme? Dijkstra's algoritme kan worden gebruikt om het kortste pad van het ene knooppunt in een grafiek naar elk ander knooppunt binnen dezelfde graafgegevensstructuur te bepalen, op voorwaarde dat de knooppunten bereikbaar zijn vanaf het startknooppunt. Dijkstra's algoritme kan worden gebruikt om de kortste weg te vinden.
Ten tweede, wat is het betere Prims- en Kruskal-algoritme?
Het algoritme van Kruskal : presteert beter intypische situaties (dunne grafieken) omdat het eenvoudigere datastructuren gebruikt. Het algoritme van Prim : is aanzienlijk sneller in de limiet als je een erg dichte grafiek hebt met veel meer randen dan hoekpunten.
Wat is de tijdscomplexiteit van het Prims-algoritme?
Het gebruikt dus een enkele array van gehele getallen om een sub-grafiek van een grafiek te definiëren. De tijd complexiteit is O(VlogV +ElogV) = O(ElogV), waardoor het hetzelfde is als Kruskal's salgoritme . Echter, Het algoritme van Prim kan worden verbeterd met behulp van Fibonacci Heaps (vgl. Cormen) naar O(E + logV).
Aanbevolen:
Waar wordt het PNG-bestandsformaat voor gebruikt?
Een PNG-bestand is een afbeeldingsbestand dat is opgeslagen in de indeling Portable Network Graphic (PNG). Het bevat een bitmap van geïndexeerde kleuren en is gecomprimeerd met lossless-compressie vergelijkbaar met a. GIF-bestand. PNG-bestanden worden vaak gebruikt om webafbeeldingen, digitale foto's en afbeeldingen met een transparante achtergrond op te slaan
Waar wordt het EAX-register voor gebruikt?
Eax is een 32-bits register voor algemene doeleinden met twee veelvoorkomende toepassingen: om de geretourneerde waarde van een functie op te slaan en als een speciaal register voor bepaalde berekeningen. Het is technisch gezien een vluchtig register, omdat de waarde niet behouden blijft. In plaats daarvan wordt de waarde ervan ingesteld op de geretourneerde waarde van een functie voordat een functie terugkeert
Waar wordt het.htaccess-bestand voor gebruikt?
Htaccess (hyperteksttoegang) is een handig bestand voor veel webservers om instellingen per directory toe te passen. Hiermee kan de standaardconfiguratie van de Apache-server tijdens runtime worden overschreven. Gebruik makend van. htaccess we kunnen elke functionaliteit tijdens runtime gemakkelijk in- of uitschakelen
Waar wordt het IP-protocol voor gebruikt?
Het Internet Protocol (IP) is het belangrijkste communicatieprotocol in de internetprotocolsuite voor het doorgeven van datagrammen over netwerkgrenzen heen. De routeringsfunctie maakt internetwerken mogelijk en brengt in wezen het internet tot stand
Waar wordt het Transmission Control Protocol voor gebruikt?
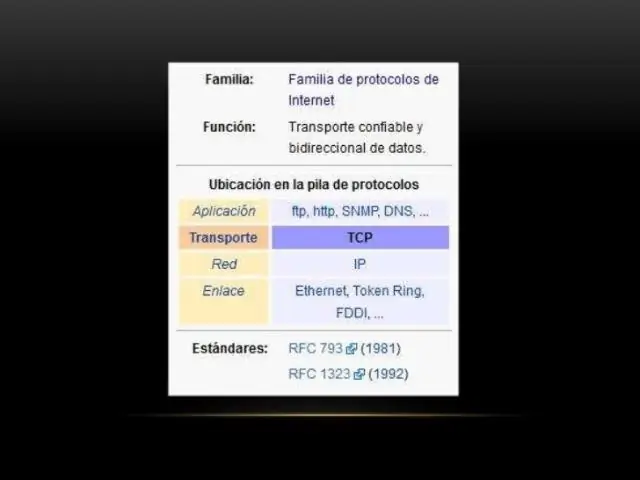
TCP/IP (Transmission Control Protocol/InternetProtocol) TCP/IP, of het Transmission ControlProtocol/Internet Protocol, is een reeks communicatieprotocollen die worden gebruikt om netwerkapparaten op internet met elkaar te verbinden. TCP/IP kan ook worden gebruikt als communicatieprotocol in een particulier netwerk (een intranet of een extranet)