Video: Wat is een symmetrieas?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
De grafiek van een kwadratische functie is een parabool. De symmetrie-as van een parabool is een verticale lijn die de parabool in twee congruente helften verdeelt. De symmetrie-as gaat altijd door het hoekpunt van de parabool. De x -coördinaat van het hoekpunt is de vergelijking van de symmetrie-as van de parabool.
Met dit in het achterhoofd, wat is de definitie van de symmetrieas?
Symmetrie-as . meer Een lijn door een vorm zodat elke zijde een spiegelbeeld is. Wanneer de vorm in tweeën wordt gevouwen langs de symmetrie-as , dan komen de twee helften overeen.
Evenzo, hoe vind je het hoekpunt en de symmetrieas? De hoekpunt Vorm van een kwadratische functie wordt gegeven door: f(x)=a(x−h)2+k, waarbij (h, k) de hoekpunt van de parabool. x=h is de symmetrie-as . Gebruik het voltooien van de vierkante methode om f(x) om te zetten in hoekpunt Formulier.
Bovendien, wat is de as van symmetrie voorbeelden?
De twee zijden van een grafiek aan weerszijden van de symmetrie-as eruit zien als spiegelbeelden van elkaar. Voorbeeld : Dit is een grafiek van de parabool y = x2 – 4x + 2 samen met zijn symmetrie-as x = 2. De symmetrie-as is de rode verticale lijn.
Wat is de topformule?
y = a(x – h)2 + k, waarbij (h, k) de. is hoekpunt . in y = ax2 + bx + c (dat wil zeggen, beide a's hebben exact dezelfde waarde). Het teken op "a" geeft aan of de kwadratische opening omhoog of omlaag gaat.
Aanbevolen:
Wat is een goede richtlijn voor het gebruik van een blikje perslucht om een pc schoon te maken?
Wat is een goede richtlijn voor het gebruik van een blikje perslucht om een pc schoon te maken? Gebruik een lange, gestage luchtstroom uit het blik. Spuit de perslucht niet met de bus ondersteboven. Gebruik geen perslucht om een CPU-ventilator schoon te maken
Wat is een proces in een besturingssysteem, wat is een thread in een besturingssysteem?
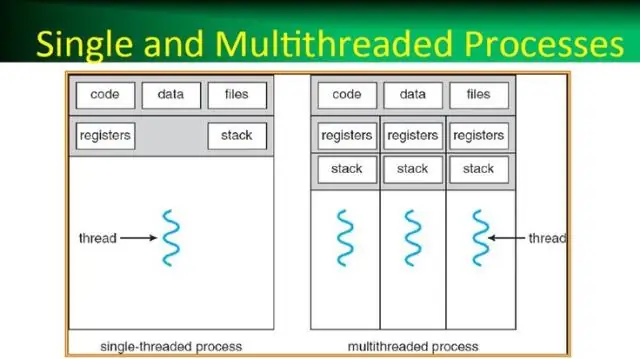
Een proces, in de eenvoudigste bewoordingen, is een uitvoeringsprogramma. Een of meer threads worden uitgevoerd in de context van het proces. Een thread is de basiseenheid waaraan het besturingssysteem processortijd toewijst. De threadpool wordt voornamelijk gebruikt om het aantal applicatiethreads te verminderen en om de workerthreads te beheren
Heeft de letter N een symmetrieas?
Letters zoals B en D hebben een horizontale symmetrielijn: hun bovenste en onderste delen komen overeen. Sommige letters, bijvoorbeeld X, H en O, hebben zowel verticale als horizontale symmetrielijnen. En sommige, zoals P, R en N, hebben geen symmetrieassen
Heeft een rechthoekige driehoek een symmetrieas?
Een rechthoekige driehoek, als het een gelijkbenige rechthoekige driehoek is, heeft deze één symmetrielijn. als het een gelijkzijdige rechthoekige driehoek is, heeft het drie symmetrieassen. als het een ongelijkzijdige rechthoekige driehoek is, heeft het geen symmetrielijn
Wat is een array, kunnen we een string en een geheel getal samen in een array opslaan?
Arrays kunnen elk type elementwaarde bevatten (primitieve typen of objecten), maar u kunt geen verschillende typen in een enkele array opslaan. U kunt een reeks gehele getallen of een reeks tekenreeksen of een reeks reeksen hebben, maar u kunt geen reeks hebben die bijvoorbeeld zowel tekenreeksen als gehele getallen bevat