Video: Wat is de diagonaal van Nonagon?
2024 Auteur: Lynn Donovan | [email protected]. Laatst gewijzigd: 2023-12-15 23:51
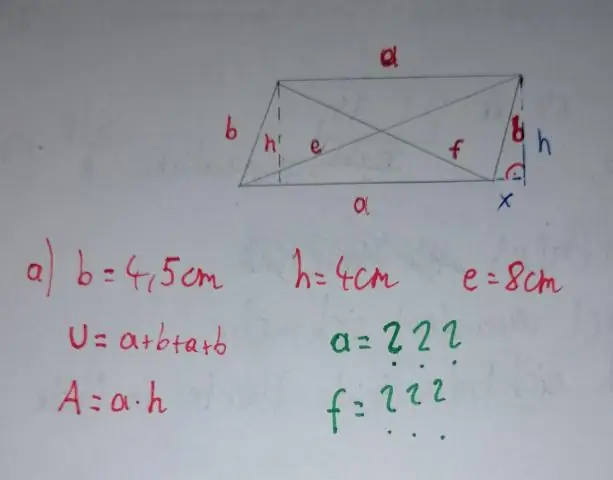
EEN nonagon , of negenhoek, is een veelhoek met negen zijden en negen hoekpunten, en heeft 27 verschillende diagonalen . De formule voor het bepalen van het aantal diagonalen van an-zijdige veelhoek is n(n - 3)/2; dus, een nonagon heeft 9(9 -3)/2 = 9(6)/2 = 54/2 = 27 diagonalen.
Evenzo kan men zich afvragen, hoeveel diagonaal heeft een Nonagon?
Bovendien, aangezien elke diagonaal verbinden twee hoekpunten, we nodig hebben de helft nemen van n(n-3) om de herhalingen van te elimineren diagonalen . Ten slotte wordt de formule 0,5n(n-3). Zet nu n op 9, het aantal diagonalen in een nonagon is gelijk aan 0,5*9*(9β3)=27.
Bovendien, wat is een Nonagon in wiskunde? Nonagon . meer Een 9-zijdige polygoon (een platte vorm met rechte zijden). (Ook wel een Enneagon genoemd) Zie: Polygoon.
Ook de vraag is, wat is diagonale formule?
Diagonale formule . Elk vierkant met twee diagonalen even lang zijn aan elkaar. DiagonaalFormule wordt gebruikt om de veelhoek te berekenen diagonalen . diagonalen zijn een lijn die twee niet-aangrenzende hoekpunten van een veelhoek verbindt, d.w.z. a diagonaal verbindt twee hoekpunten van een veelhoek exclusief de randen van de figuur.
Hoe vind je diagonalen?
Tot vind het totale aantal diagonalen in apolygoon, vermenigvuldig het aantal diagonalen per hoekpunt (n - 3) door het aantal hoekpunten, n, en deel door 2 (anders elk diagonaal wordt dubbel geteld).
Aanbevolen:
Wat is een diagonaal in een ruit?
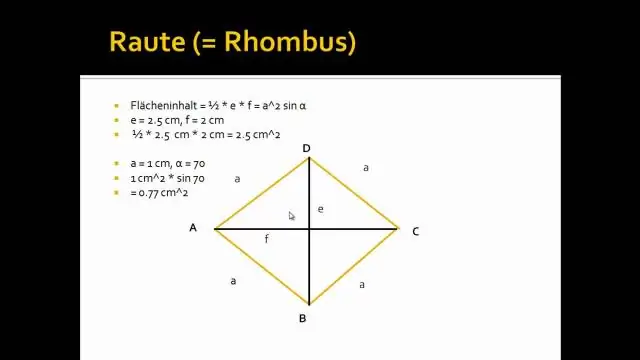
Diagonalen van een ruit In elke ruit snijden de diagonalen (lijnen die tegenover elkaar liggende hoeken met elkaar verbinden) elkaar in een rechte hoek (90°). Dat wil zeggen, elke diagonaal snijdt de andere in twee gelijke delen, en de hoek waar ze elkaar kruisen is altijd 90 graden
Welke van de volgende is een voordeel van het gebruik van visuele hulpmiddelen in een toespraak?
De belangrijkste voordelen van het gebruik van visuele hulpmiddelen in uw toespraken zijn dat ze de belangstelling van het publiek vergroten, de aandacht van de spreker afleiden en de spreker meer vertrouwen geven in de presentatie als geheel
Wat is de straf in India voor het stelen van activa van computerdocumenten of de broncode van software van een organisatie-individu of van enig ander middel?
Uitleg: De straf in India voor het stelen van computerdocumenten, activa of de broncode van software van een organisatie, persoon of op enige andere manier is 3 jaar gevangenisstraf en een boete van Rs. 500.000
Wat zijn de belangrijkste onderdelen van bestandsbeheer. Vink alles aan wat van toepassing is?
De belangrijkste componenten van bestandsbeheer zijn de opslag van gegevens, de bestandsmetadata en het bestandssysteem. Wat zijn de belangrijkste onderdelen van bestandsbeheer? Vink alles aan wat van toepassing is. U kunt veel processen voor één programma laten draaien
Wat zijn enkele voorbeelden van soorten seksistisch taalgebruik en wat is de impact van die voorbeelden?
Wat zijn enkele voorbeelden van soorten seksistisch taalgebruik en wat is de impact van die voorbeelden? A: Om een paar voorbeelden van seksistische taal te noemen, zijn: "actrice", "zakenman", "visser", "serveerster". Ze kunnen worden ontvangen als zeer aanstootgevend en discriminerend